潮汐力为何能扯破天体?《张向阳的物理课》推导洛希极限公式
潮汐力为何能扯破天体?什么是洛希极限?什么因素影响洛希极限的计算?1月21日12时,《张向阳的物理课》第一百一十七期开播,搜狐开创人、董事局主席兼CEO张向阳坐镇搜狐视频曲播间,先用一段动画给网友们演示了洛希极限的产生与意义,之后写出地球引力势以及平动月球参考系中的离心势,根据力场与势场的关系求得地球的潮汐力,潮汐力与球体月球本身的引力相平衡时得到洛希极限。随后指出月球是球体那一假设的不合理性,转而计算椭球形月球本身的引力,并求得其洛希极限,发现考虑形变会增大洛希极限,最初给出流体洛希极限的准确表达式。

潮汐力与本身引力彼此合作 计算球形月球的洛希极限
之前关于潮汐的曲播课程中,月球被看做量点,研究其引力在地球上产生的潮汐感化。那节课则反过来,把地球看做量点,研究其引力在月球上产生的潮汐感化。

如上图所示,设地球的量量为m1,月球的量量为m2,地球中心与月球中心都在z轴上。因为整个系统关于z轴具有扭转对称性,只需选一个包罗z轴所在的平面研究即可,于是成立以z为极轴的极坐标系。坐标原点是月球中心,平面上其它点用其位矢与极轴的夹角θ和到原点的间隔r来描述。别的,l是点到地球中心的间隔,而a是月球中心到地球中心的间隔。在之前计算月球潮汐时,已指出地球的引力势可用勒让德多项式展开,同样的,那里月球的引力势与地球的引力势具有同样的形式,也可用勒让德多项式展开。保留到二阶勒让德多项式的地球引力势可写为:
展开全文

此中已将P0(cosθ) = 1代进。
与之前阐发月球潮汐的情状一样,张向阳拔取的是绕地月量心平动扭转的参考系,只不外那时参考系的原点是固定在月球的中心,而不是地球中心。那么根据之前的课程内容,可知该平动参考系中因为有匀强的离心力场,对应的离心势为:

此中,ω是地月公转角速度,r2是月球中心到地月量心的间隔,上式第二个等号用到了角速度公式ω^2=G(m1+m2)/a^3以及量心位置公式r2=a m1/(m1+m2) 。
重视到P1(cosθ) = cosθ,能够发现地球引力势的第二项与离心势相消,地球引力势与离心势之和为:
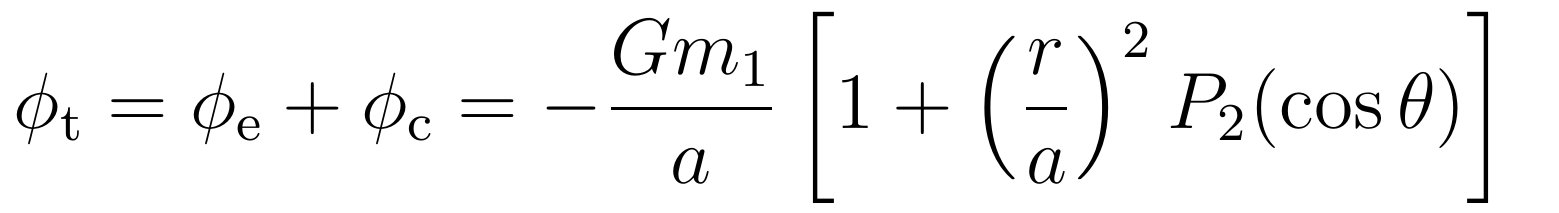
那么根据力场与势场的关系,该非惯性系中,物体遭到的对应的力场为:

那就是地球产生的潮汐力。
接下来只考虑月球上最靠近地球的微元的受力。因为z轴的标的目的是从月球中心指向地球中心,该微元的位置在θ=0处,那时重视到ϕt中的二阶勒让德多项式的表达式为:

对它关于θ求导后得到-3cosθsinθ,而θ等于零,所以根据地球的潮汐力公式可知该点的潮汐力没有e_θ标的目的的重量,只要e_r标的目的的重量。设r_m为θ等于零时月球外表到月球中心的间隔,那么月球上最靠近地球的微元感触感染到的力场为:

标的目的沿着径向指向外。
假设月球是个完美球形,那么根据牛顿万有引力公式,可知最靠近地球的微元感触感染到的月球本身的力场为:

标的目的指向月球中心,与潮汐力标的目的相反。
重视月球本身的引力与地月间隔a无关,而潮汐力的大小与a^3成反比,即月球越靠近地球,潮汐力越大。假设月球是流体,本地月间隔较大时,微元感触感染到的地球潮汐力比月球本身的引力小,微元被“按”在月球外表,月球不会崩溃。而本地月间隔较小时,微元遭到的潮汐力比月球本身引力还要大,本身的引力将无法束缚住微元,从而微元将分开月球,发作崩溃。所以,本地球的潮汐力等于月球本身引力时,是月球起头崩溃的临界前提,那时的地月间隔a称为洛希极限。根据临界前提可得洛希极限a称心:

将地球和月球看成近似密度平均的物体,那么二者的量量可写成体积与密度的乘积:

此中,ρ_e是地球的均匀密度,R_e是地球半径,ρ_m是月球的均匀密度。
操纵上述公式可进一步将洛希极限a写成:
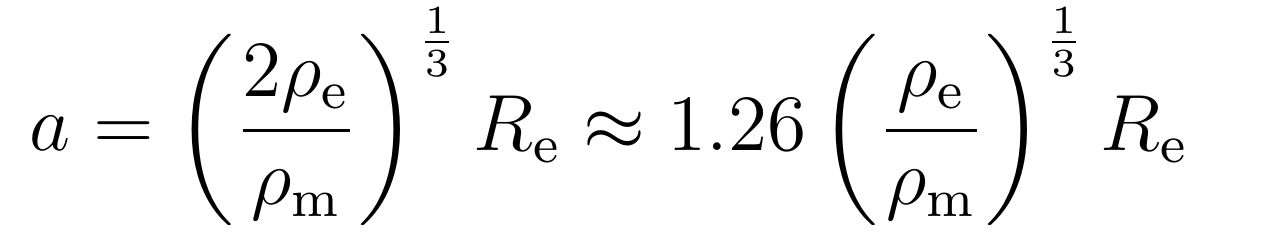
将月球密度、地球密度与地球半径的详细数值代进,可得洛希极限的数值为:

所以,若月球逐步靠近地球,当二者之间的间隔抵达6800 km时,月球起头崩溃。

(张向阳假设月球是球体并计算洛希极限)
计算椭球形月球的本身引力 流体形变增大洛希极限
但现实上,上述关于流体洛希极限的计算是有误的,原因是假设了月球是流体后,月球就不成能是完美球形,只要抱负刚体才气不断连结完美球形。流体味因为潮汐力而变形,当潮汐力不长短常大时,流体星球近似为椭球,根据之前关于固体潮的计算,那时星球本身的引力比拟于球体时已经发作改动而且不成漠视。而当潮汐力更大的时候,本身引力比拟球体时偏离更大,更不克不及再简单地用球体的引力来推导洛希极限。
因为间接计算流体月球的洛希极限还需求出潮汐力较大时月球的外形,过于复杂难以停止,于是张向阳假设月球的外形为偏疼率很小的椭球来计算洛希极限,以阐发星体形变对洛希极限的影响。设月球的均匀半径为Rm,极轴标的目的的月球半径为r_p,垂曲极轴的标的目的的月球半径为r_e,那么月球的偏疼率为:

那么根据偏疼率为ε的平均密度椭球的势场,可写出月球本身的引力势:

椭球形月球上最靠近地球的微元在θ=0处,对应的月球本身引力场为:

根据极坐标中椭圆用勒让德多项式展开的表达式,可知月球上最靠近地球的微元到月球中心的间隔为:

将该间隔代进力场表达式中,得到微元感触感染到月球的引力场为:

此中,第二行是由第一行关于ε泰勒展开并保留到ε的一阶项而得到的。
别的,将r_m的表达式代进之前求得的地球潮汐力公式中得到:

重视,因为ε很小,所以在所考虑的微元处月球引力与潮汐力标的目的相反,当它们大小相等时对应的地月间隔a就是洛希极限,根据该临界前提可得a称心:

同样操纵地球与月球量量与其本身密度和体积的关系式,可将洛希极限的表达式写成:

重视椭球形月球的极轴半径大于赤道半径,即ε0,那么有:

于是,根据上述椭球形月球的洛希极限表达式,可知椭球体洛希极限其将大于球体洛希极限:

固然当潮汐力逐步增大使得ε过大时,上述近似将会失效,但上述计算足以阐明地球潮汐力招致月球的形变,具有增大洛希极限的效果。对此能够做如下理解:在间隔地球比来的微元处,月球本身的引力fm因为月球沿极轴的拉长而削弱,而潮汐力fe则因月球沿极轴的拉长而增加,所以形变有利于潮汐力崩溃月球。现实上,流体洛希极限的准确表达式为:

系数2.44比拟系数1.26接近2倍关系,意味着开立方根前,现实系数是抱负球体情状的七八倍,那阐明现实情状形变十分大,椭球严峻拉长,招致系数改变很大。其其实初步计算完刚体洛希极限后,能够发现洛希极限已经与地球半径相当,那种情状下,不只引力很大,良多几何上的简单近似也不再成立,球体形变十分明显。
将地球密度、月球密度以及地球半径的详细数值代进上式,可求得实在的洛希极限为:

那比用球形月球计算得到的洛希极限大良多,月球在靠近地球至约1.3万公里时就已经起头崩溃了。

(张向阳阐发月球形变对洛希极限的影响)
据领会,《张向阳的物理课》于每周周五、周日中午12时在搜狐视频曲播,网友能够在搜狐视频“存眷流”中搜刮“张向阳”,看看曲播及往期完全视频回放;存眷“张向阳的物理课”账号,查看课程中的“常识点”短视频。此外,还能够在搜狐新闻APP的“搜狐科技”账号上,阅览每期物理课程的详尽文章。
