美女与汉子的游戏：看似公允的收割办法。博弈论与纳什平衡（六）

列位同窗各人好！我是李永乐教师。之前我讲了几期博弈论，没看过的小伙伴能够点击：

策梅洛定理：游戏起头时，结局就定了！

囚徒窘境：你会变节你的伴侣吗？

胆怯鬼博弈：若何制止世界大战？

海盗分金币问题：你能拿到几钱？

田忌赛马：盘算能否填补实力的差距？

你炒股吗？总有同窗跟我说，本身明明是个散户，但是却能撬动整个大盘。本身卖了大盘就涨，本身买了大盘就跌，那是怎么回事呢？

有一个有趣的博弈论例子，和我们在股市的遭遇很像。那个例子是如许的：

有一个汉子在酒吧里饮酒，一位美女走过来，对他说：我们玩个游戏吧。规则如下：

我们每小我手里各拿一个硬币，不让对方晓得的扣在桌子上。然后两人同时把手拿开，看硬币的正背面。假设两枚硬币都是正面，那么美女给汉子3块钱。假设都是背面，那么美女给汉子1块钱。假设硬币是一正一反，汉子给美女两块钱。

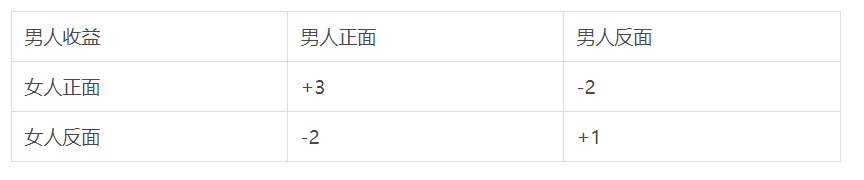
请问，汉子应该参与那个游戏吗？假设两边不断玩下往，是不是会没输没赢呢？

假设只利用概率论，很随便觉得那是一个公允的游戏。因为假设两小我都是随机出牌，那么两个都正面的概率为1/4，两个都背面概率为1/4，一正一反概率为1/2，根据概率和期看的含义，一次游戏中汉子收益的数学期看就是0。

也就是说：颠末一次游戏，汉子均匀回报为零，既不赚钱，也不亏钱。

事实实的如斯吗？

在那个游戏中，汉子和女人并非抛硬币，而是本身抉择出硬币正面仍是背面，显然，汉子和女人都不成能不断出正面或者不断出背面，因为如许会被敌手摸出法例。但是他们仍然能够在屡次游戏中将本身正面的频次设定为某个值四周，从而获得统计意义上的收益，从而使得游戏就从一个概率问题，酿成了一个博弈问题，那个固定的频次就是混合战略的纳什平衡。

展开全文

可是那个频次若何计算呢？

我们假设汉子的战略是：出正面的频次为x，出背面的概率为1-x；

假设女人的战略是:出正面的频次为y，出背面的频次为1-y。

游戏中各类情状下的概率表格如图所示。

用每种情状下汉子的收益乘以概率，再把它们相加，就能计算出汉子的收益期看：

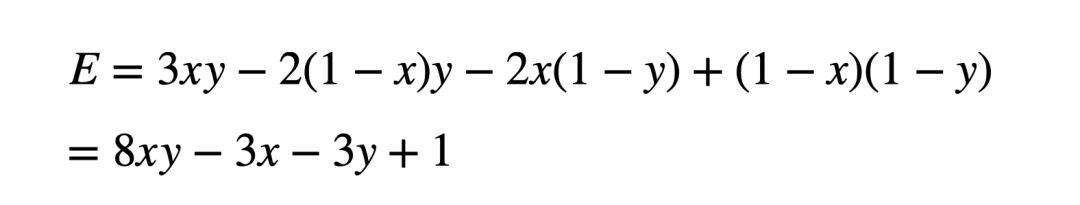
两人对那个期看值E是有差别预期的：

女人期看汉子不断赔钱，所以期看汉子收益的期看E越小越好。

汉子期看本身不断赢钱，所以期看本身的收益期看E是正的，越大越好。

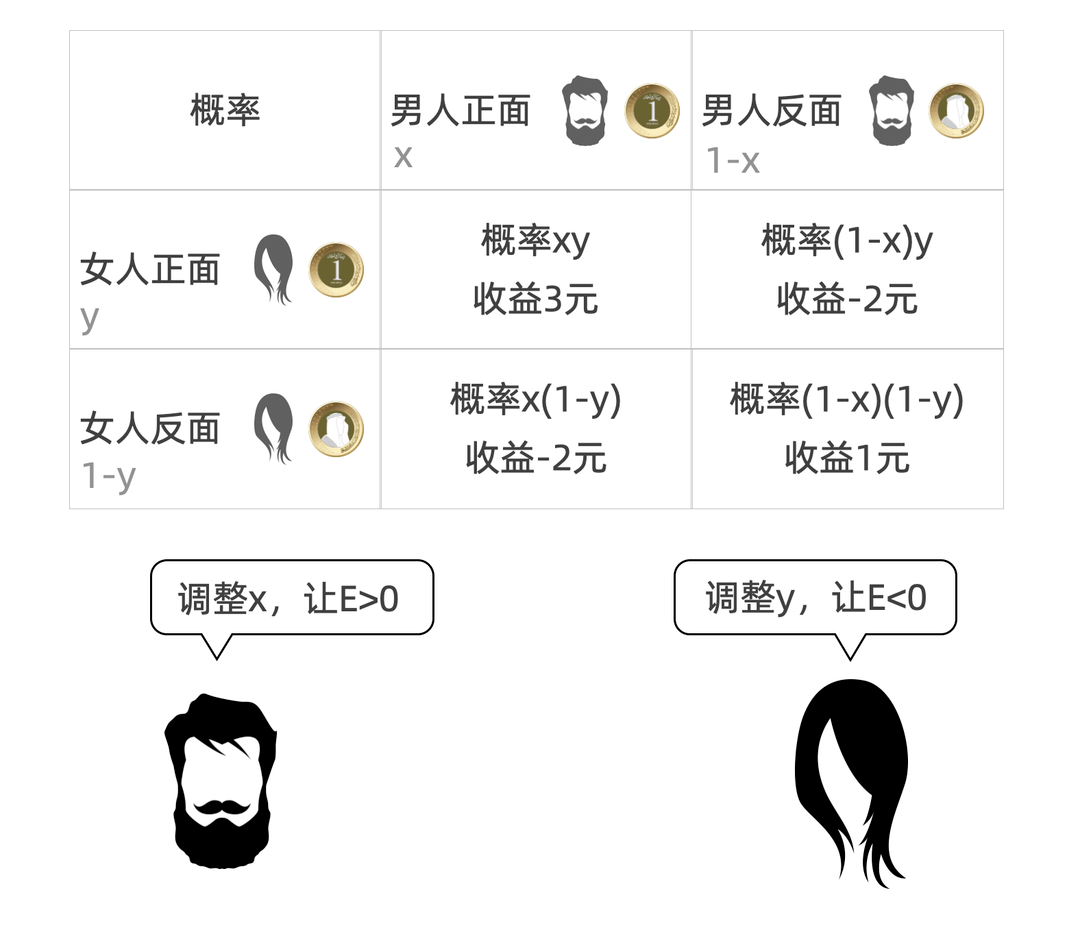
我们无妨先从女人的角度考虑吧：她事实应该让本身的y取几，才气让汉子的期看收益E最小呢？我们把表达式做一个变形：

E=(8y-3)x-3y+1

女人会想：

假设我的战略中y3/8，那么8y-3就是正的。E会跟着x的增大而增大，所以汉子发现本身的套路后，就会让x=1，如许一来汉子的收益期看就是E=5y-2。因为y3/8，所以E-1/8。汉子均匀玩一局，输的钱不超越1/8元。

假设我的战略中y3/8呢，那么8y-3就是负的，E会跟着x的减小而增大，汉子发现本身的套路后，就会让x=0，如许一来，汉子的期看就是E=1-3y。因为y3/8，所以E-1/8，汉子输的前不会超越1/8元。

假设我的战略是y=3/8呢，如许E=1-3y=-1/8，无论汉子摘用什么战略，他玩一局就输1/8元。

综上所述，对女人来讲，更优战略就是y=3/8，如许无论汉子怎么做，每一局均匀城市输掉1/8元。

那么，汉子又会若何根究呢？他也期看调整x，让本身的期看E更大。他会把公式如许变形：

E=(8x-3)y-3x+1

根据与适才女人类似的讨论，汉子最末也会摘取x=3/8的战略，那时无论女人摘用什么战略，汉子的收益期看E都更大，那个更大值是-1/8,也就是虽然汉子找到了更优的战略，均匀一局仍是会输掉1/8元。

如许，两边混合战略纳什平衡就找到了：他们城市以3/8频次出正面，5/8的频次出背面，均匀一局汉子亏掉1/8元。那个游戏对汉子是倒霉的，他永久没办法通过本身的伶俐才智获得正的收益。

怎么样，有没有倾覆你的认知？

数学题做到那了，各人从那个问题上可以获得什么启迪呢？

相信许多同窗都有股市的投资履历。在股市中，农户能够把持股价上下翻飞，让你的心痒痒的，就似乎美女一般。在农户拉升股价时，我们做多，就能够盈利。农户打压股价时，我们做空，也能够盈利。但是假设农户做多我们做空，或者相反，就会吃亏。在如许的规则下，每小我都觉得本身可能是个幸运儿，能够通过本身的命运或者战略获得正的收益。

但是事实上，农户有比散户更强的控盘才能和模子计算才能，他们会摘用一种更好的战略，使得散户无论摘取什么体例炒股，统计意义上城市赔钱。当然不肃清有些散户的命运特殊好，在一段时间内大赚了一笔。但即使如斯，我们仍然要说，在如许的规则下，持久炒股的散户，才会大都都赔钱。

别问我为什么有那么深入的领略。

存眷我，听我陆续闲谈博弈论。