R语言广义相加模子 (GAMs)阐发揣测CO2时间序列数据|附代码数据

全文下载链接：

比来我们被客户要求撰写关于广义相加模子 (GAMs)的研究陈述，包罗一些图形和统计输出。

情况科学中的许大都据不合适简单的线性模子，更好用广义相加模子（GAM）来描述

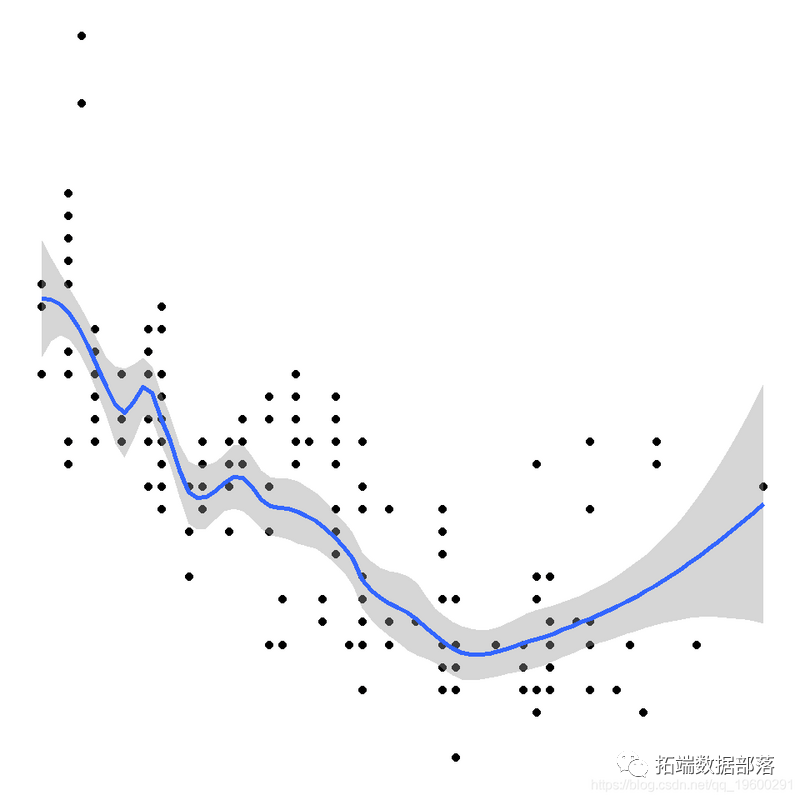
那根本上就是具有 光滑函数的广义线性模子（GLM）的扩展 。当然，当您利用光滑项拟合模子时，可能会发作许多复杂的工作，但是您只需要领会根本原理即可。

理论

让我们从高斯线性模子的方程起头 ：

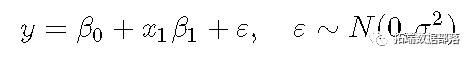
GAM中发作的改变是存在光滑项：

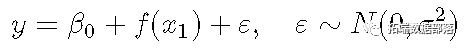
展开全文

那仅意味着对线性揣测变量的奉献如今是函数f。从概念上讲，那与利用二次项（）或三次项（）做为揣测变量没什么差别。

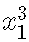
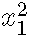
在那里，我们将重点放在样条曲线上。在过往，它可能类似于分段线性函数。

例如，您能够在模子中包罗线性项和光滑项的组合

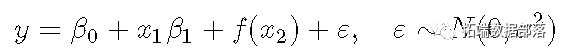
或者我们能够拟合广义散布和随机效应

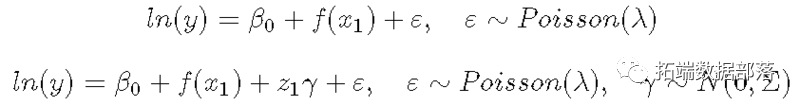
一个简单的例子

让我们测验考试一个简单的例子。起首，让我们创建一个数据框，并创建一些具有明显非线性趋向的模仿数据，并比力一些模子对该数据的拟合水平。

x - seq(0, pi * 2, 0.1)

sin_x - sin(x)

y - sin_x + rnorm(n = length(x), mean = 0, sd = sd(sin_x / 2))

Sample - data.frame(y,x)

library(ggplot2)

ggplot(Sample, aes(x, y)) + geom_point()

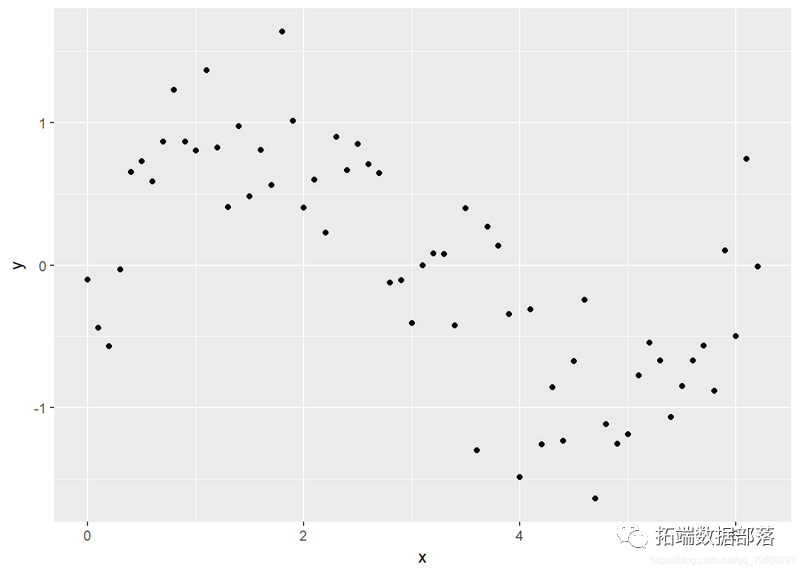
测验考试拟合通俗的线性模子：

lm_y - lm(y ~ x, data = Sample)

并利用geom_smooth in 绘造带有数据的拟合线 ggplot

ggplot(Sample, aes(x, y)) + geom_point() + geom_smooth(method = lm)

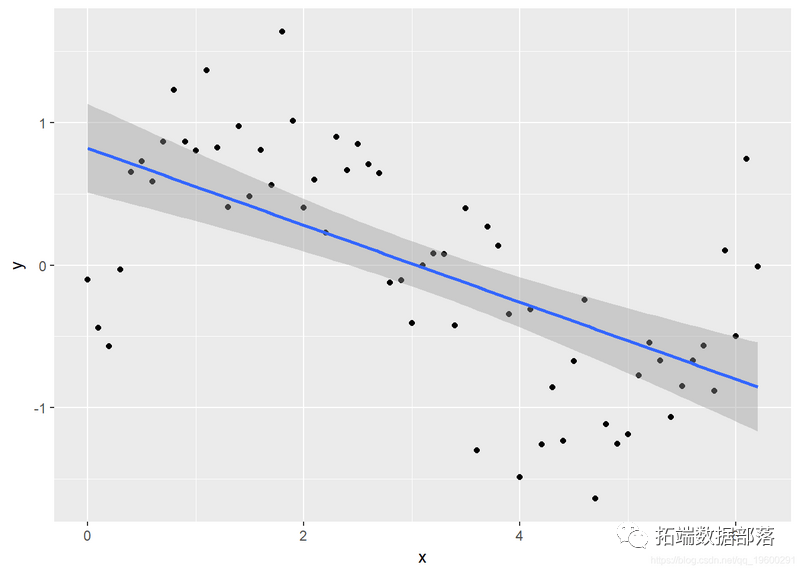
查看图或 summary(lm_y)，您可能会认为模子拟合得很好，但请查看残差图

plot(lm_y, which = 1)

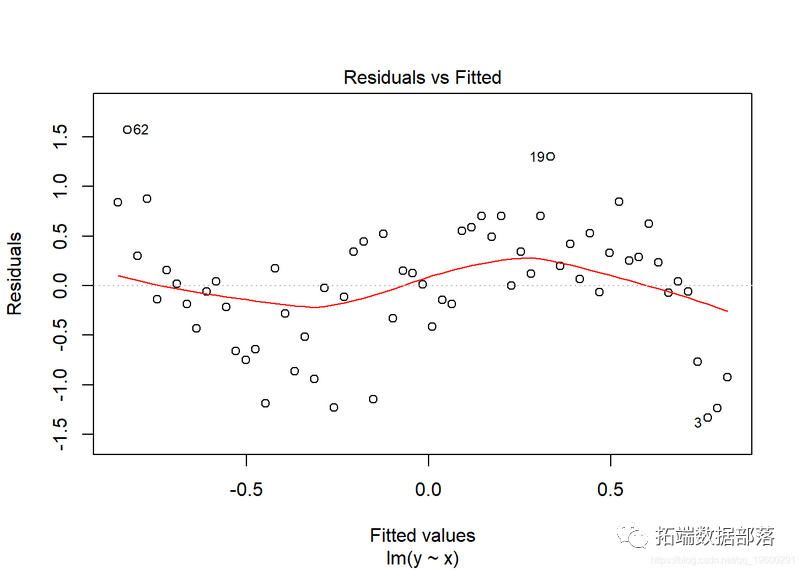
显然，残差未平均散布在x的值上，因而我们需要考虑一个更好的模子。

点击题目查阅往期内容

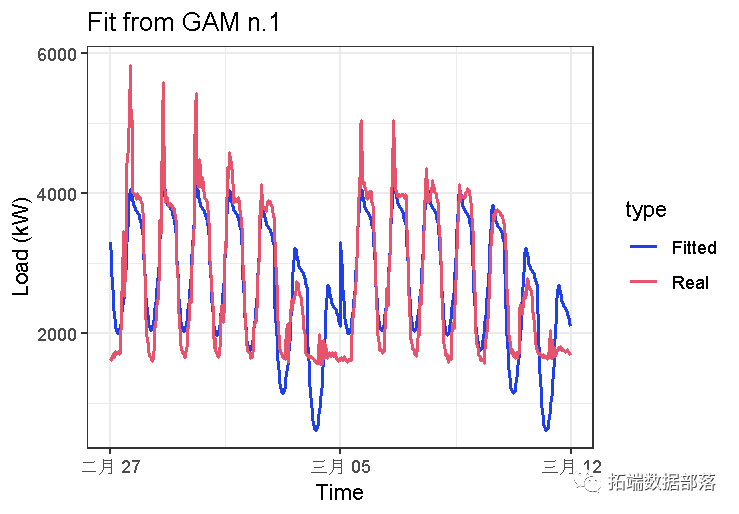
【视频】广义相加模子（GAM）在电力负荷揣测中的利用

摆布滑动查看更多

01

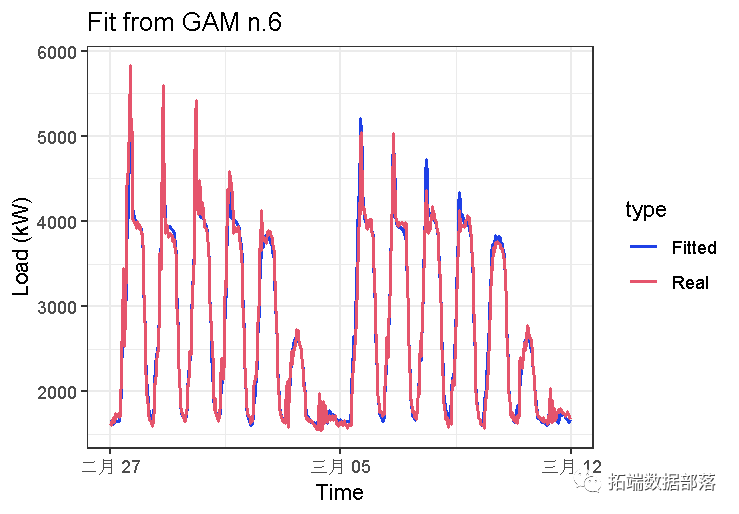
02

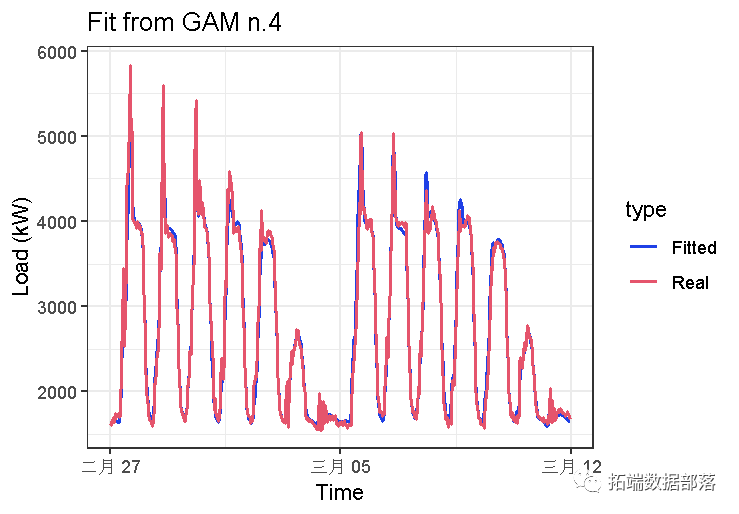
03

04

运行阐发

在R中运行GAM。

要运行GAM，我们利用：

gam_y - gam(y ~ s(x), method = "REML")

要提取拟合值，我们能够predict ：

predict(gam_y, data.frame(x = x_new))

但是关于简单的模子，我们还能够操纵中的 method = 参数来 geom_smooth指定模子公式。

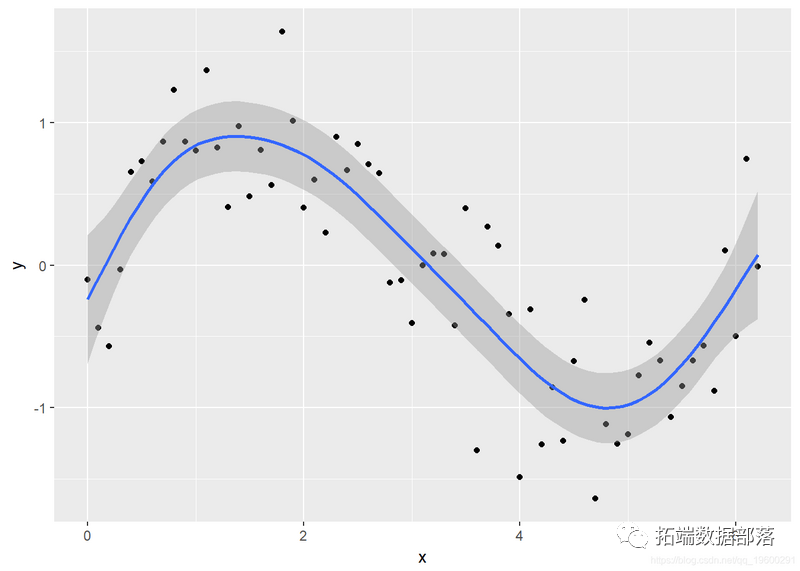
您能够看到该模子更合适数据，查抄诊断信息。

check.gam 快速简便地查看残差图。

gam.check(gam_y)

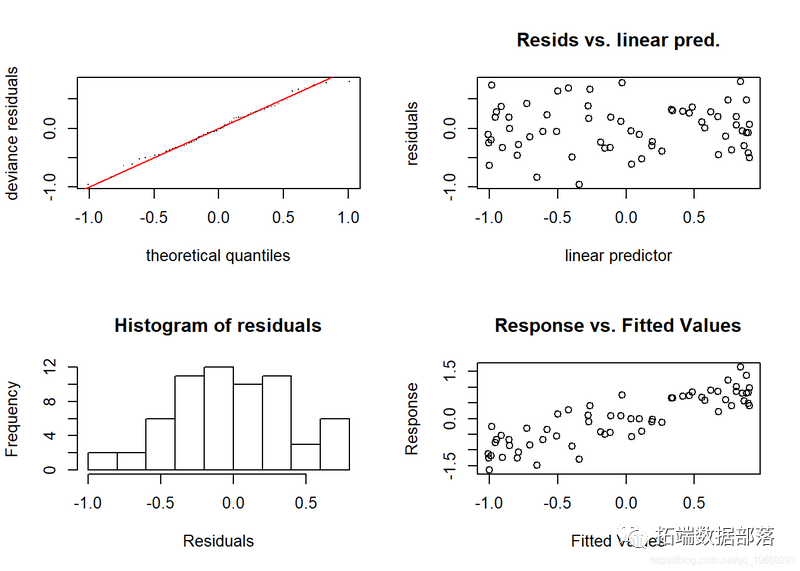
## Method: REML Optimizer: outer newton

## full convergence after 6 iterations.

## Gradient range [-2.37327e-09,1.17425e-09]

## (score 44.14634 scale 0.174973).

## Hessian positive definite, eigenvalue range [1.75327,30.69703].

## Model rank = 10 / 10

## Basis dimension (k) checking results. Low p-value (k-index1) may

## indicate that k is too low, especially if edf is close to k'.

## k' edf k-index p-value

## s(x) 9.00 5.76 1.19 0.9

对模子对象利用summary将为您供给光滑项（以及任何参数项）的意义，以及阐明的方差。在那个例子中，十分适宜。“edf”是估量的自在度——素质上，数量越大，拟合模子就越扭捏。大约为1的值趋势于接近线性项。

## Family: gaussian

## Link function: identity

## Formula:

## y ~ s(x)

## Parametric coefficients:

## Estimate Std. Error t value Pr(|t|)

## (Intercept) -0.01608 0.05270 -0.305 0.761

## Approximate significance of smooth terms:

## edf Ref.df F p-value

## s(x) 5.76 6.915 23.38 2e-16 ***

## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

## R-sq.(adj) = 0.722 Deviance explained = 74.8%

## -REML = 44.146 Scale est. = 0.17497 n = 63

光滑函数项

如上所述，我们将重点介绍样条曲线，因为样条曲线是最常实现的光滑函数（十分快速且不变）。那么，当我们指定s(x)时现实发作了什么 ？

好吧，那就是我们说要把y拟合为x个函数集的线性函数的处所。默认输进为薄板回回样条-您可能会看到的常见样条是三次回回样条。三次回回样条曲线具有 我们在议论样条曲线时想到的传统 结点–在那种情状下，它们平均散布在协变量范畴内。

基函数

我们将从拟合模子起头，记住光滑项是一些函数的和，

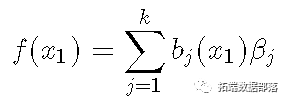
起首，我们提取_根本函数_集 （即光滑项的bj（xj）部门）。然后我们能够画出第一和第二基函数。

model_matrix - predict(gam_y, type = "lpmatrix")

plot(y ~ x)

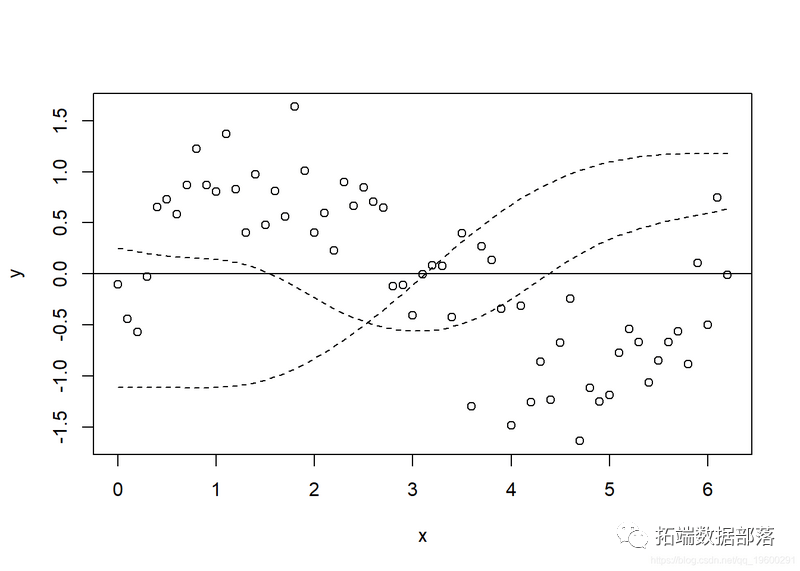
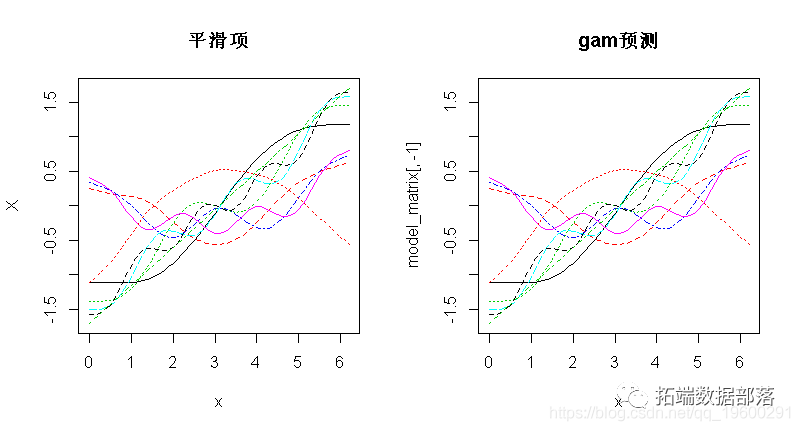
如今，让我们绘造所有基函数的图，然后再将其添加到GAM（y_pred）的揣测中。

matplot(x, model_matrix[,-1], type = "l", lty = 2, add = T)

lines(y_pred ~ x_new, col = "red", lwd = 2)

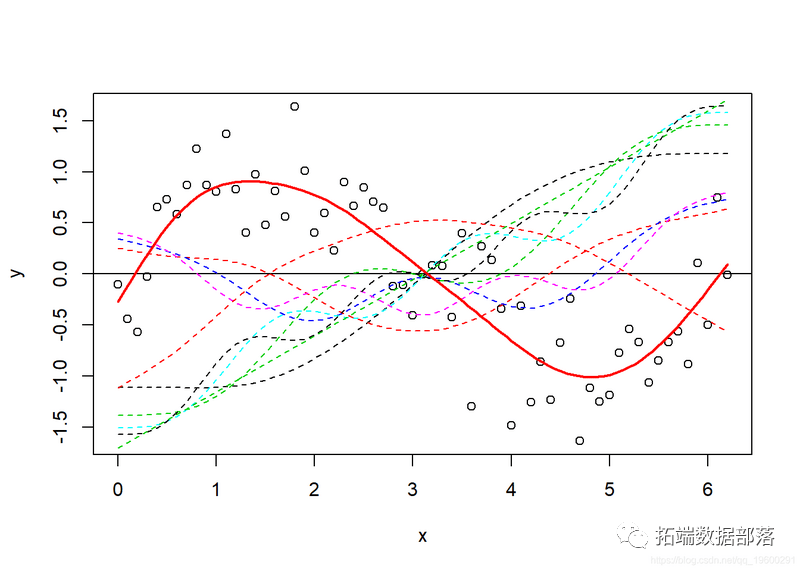
如今，最随便想到如许-每条虚线都代表一个函数（bj），据此 gam 预算系数（βj），将它们相加即可得出对应的f（x）的奉献（即先前的等式）。关于此示例而言，它很好且简单，因为我们仅根据光滑项对y停止建模，因而它是相当相关的。趁便说一句，您也能够只利用 plot.gam 绘造光滑项。

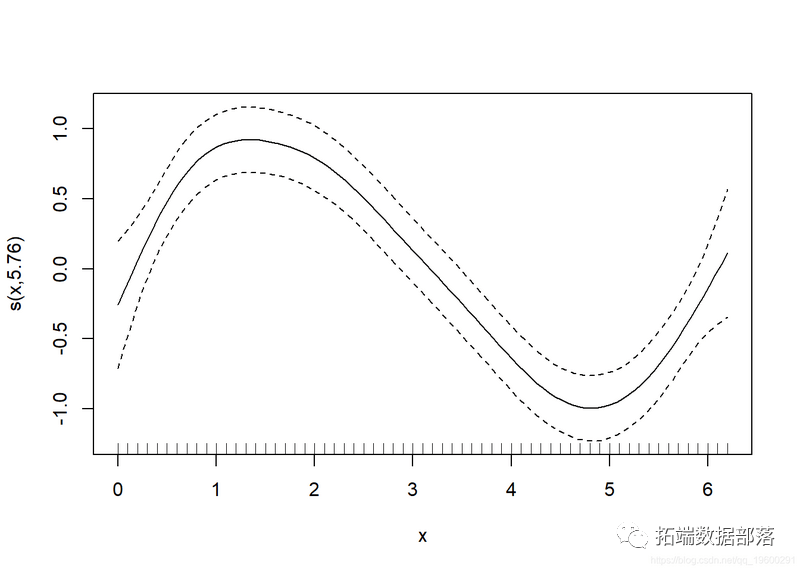
好的，如今让我们更详尽地领会基函数的构造体例。您会看到函数的构造与因变量数据是分隔的。为了证明那一点，我们将利用 smoothCon。

x_sin_smooth - smoothCon(s(x), data = data.frame(x), absorb.cons = TRUE)

如今证明您能够从根本函数和估量系数到拟合的光滑项。再次重视，那里简化了，因为模子只是一个光滑项。假设您有更多的项，我们需要将线性揣测模子中的所有项相加。

betas - gam_y$coefficients

linear_pred - model_matrix %*% betas

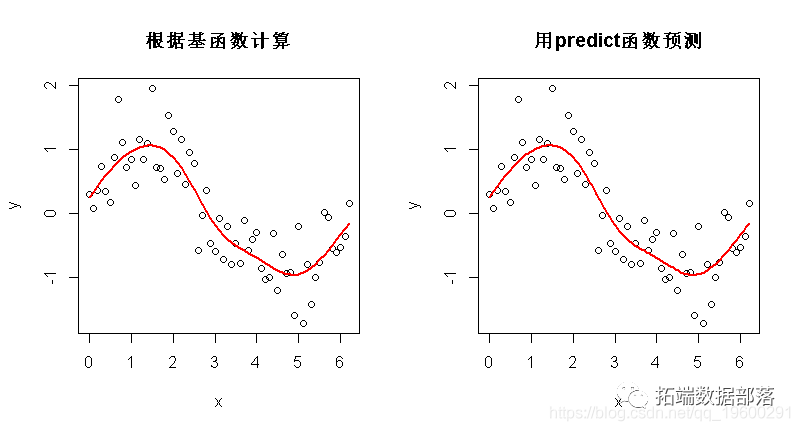
请看下面的图，记住那 X 是基函数的矩阵。

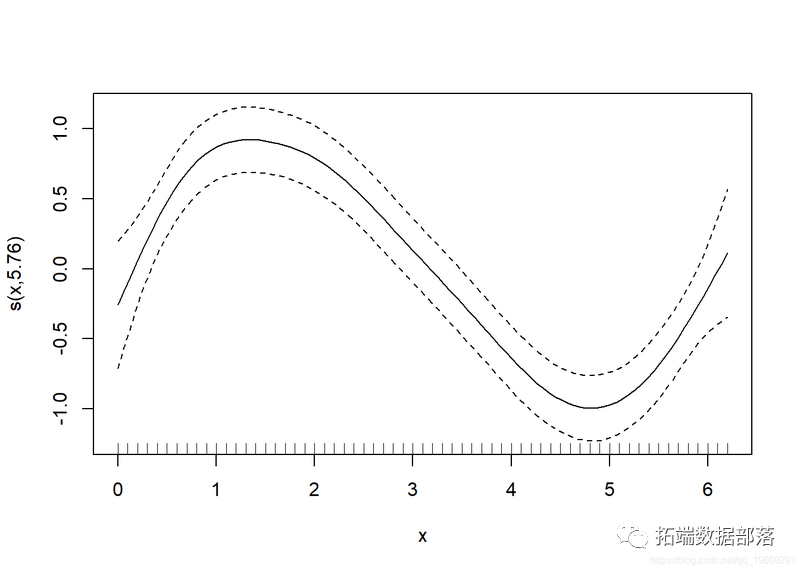
通过 gam.models ， smooth.terms 光滑模子类型的所有选项，根本函数的构造体例（赏罚等），我们能够指定的模子类型（随机效应，线性函数，交互感化）。

实在例子

我们查看一些CO2数据，为数据拟合几个GAM，以测验考试区分年度内和年度间趋向。

起首加载数据 。

CO2 - read.csv("co2.csv")

我们想起首查看年趋向，因而让我们将日期转换为持续的时间变量（摘用子集停止可视化）。

CO2$time - as.integer(as.Date(CO2$Date, format = "%d/%m/%Y"))

我们来绘造它，并考虑一个平稳的时间项。

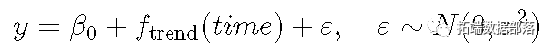
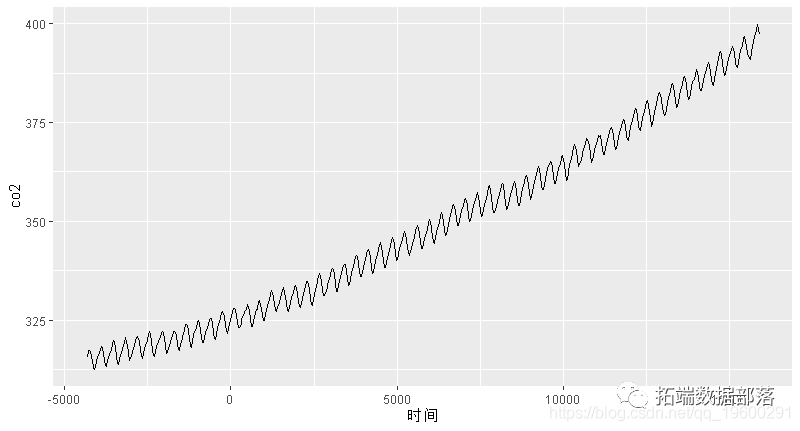
我们为那些数据拟合GAM

它拟合具有单个光滑时间项的模子。我们能够查看以下揣测值：

plot(CO2_time)

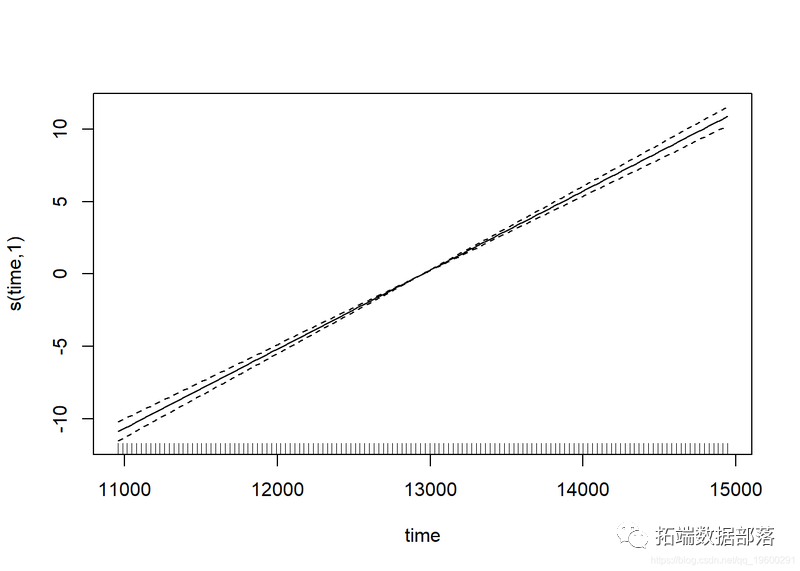
请重视光滑项若何削减到“通俗”线性项的（edf为1）-那是赏罚回回样条曲线的长处。但假设我们查抄一下模子，就会发现有些工具是紊乱的。

par(mfrow = c(2,2))

gam.check(CO2_time)

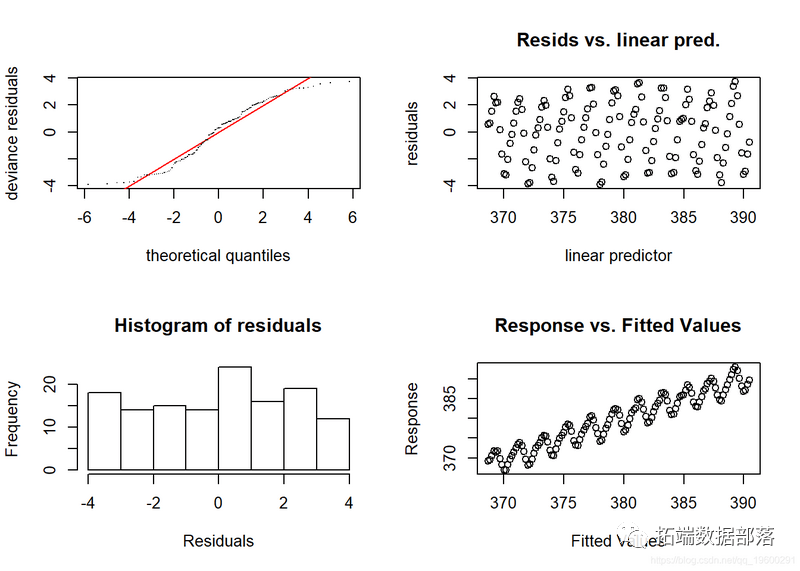
残差图的上升和下降形式看起来很希罕-显然存在某种依靠关系构造（我们可能会揣测，那与年内颠簸有关）。让我们再试一次，并引进一种称为周期光滑项。

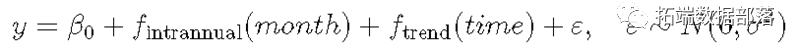
周期性光滑项fintrannual（month）由基函数构成，与我们已经看到的不异，只是样条曲线的端点被约束为相等，那在建模时是有意义的周期性（跨月/跨年）的变量。

如今，我们将看到 bs = 用于抉择光滑器类型的k = 参数和用于抉择结数的 参数，因为三次回回样条曲线具有固定的结数。我们利用12结，因为有12个月。

s(month, bs = 'cc', k = 12) + s(time)

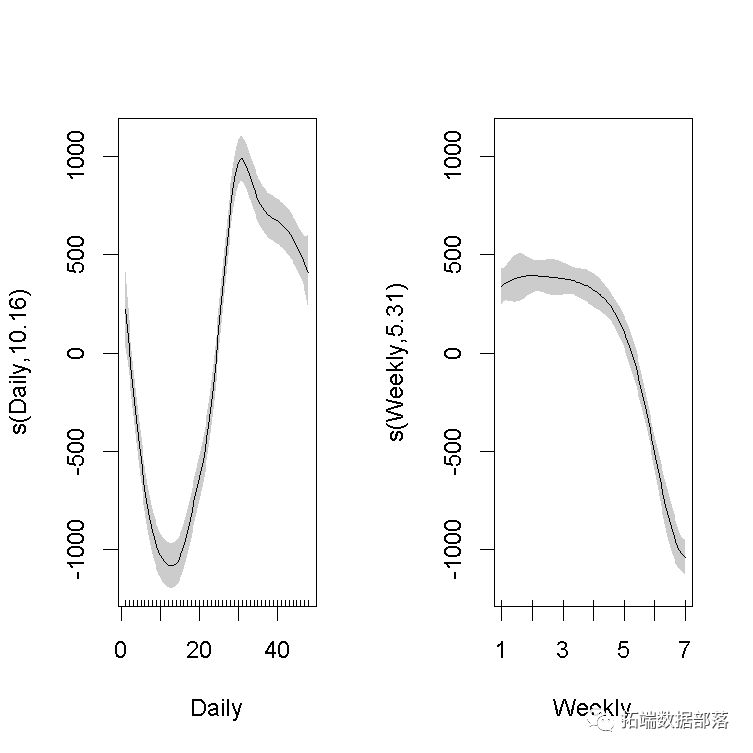
让我们看一下拟合的光滑项：

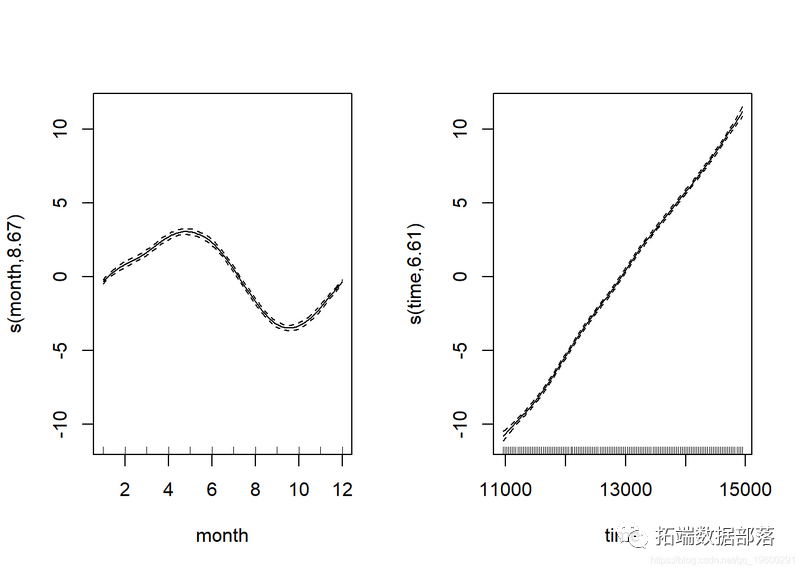
从那两个光滑项来看，我们能够看到，月度光滑项检测到CO2浓度的月度上升和下降——从相对幅度（即月度颠簸与持久趋向）来看，我们能够看出消弭时间序列成分是多么重要。让我们看看如今的模子诊断是如何的：

par(mfrow = c(2,2))

gam.check(CO2_season_time)

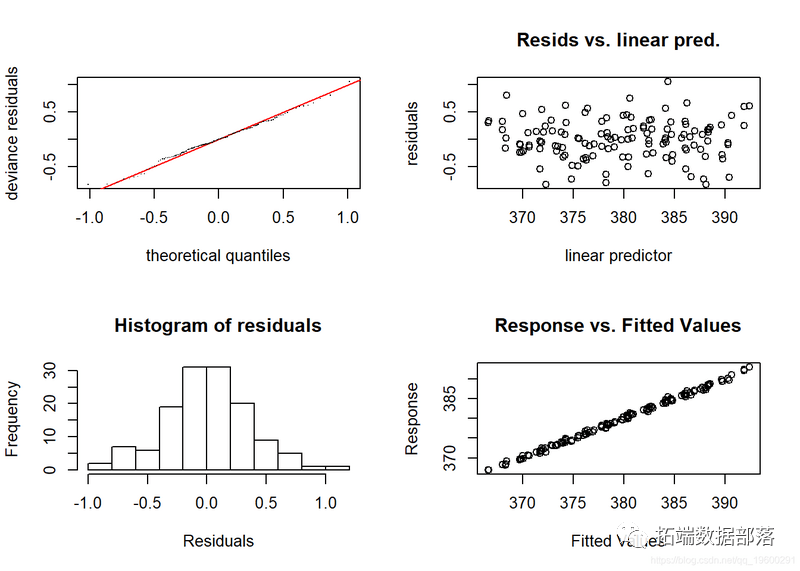
好多了。让我们看一下季节性因素若何与整个持久趋向相对应。

plot(CO2_season_time)

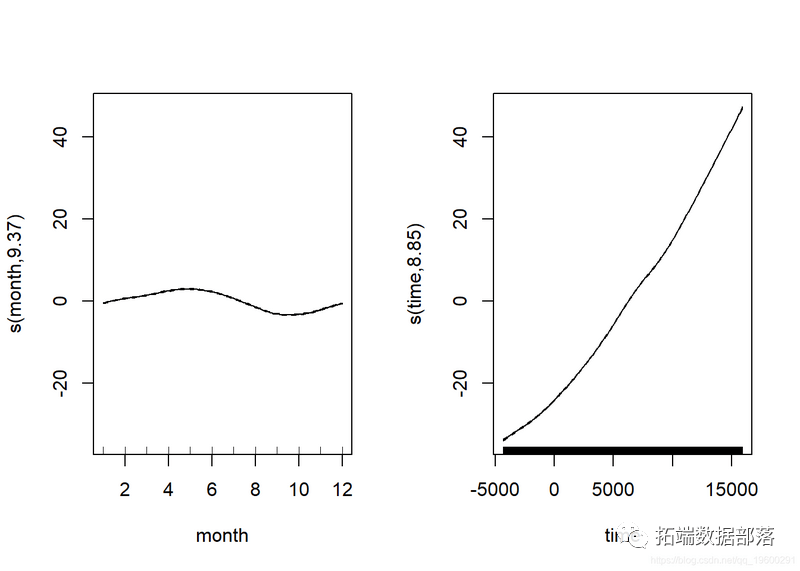
成果

从素质上讲，您能够将GAM的模子成果表达为任何其他线性模子，次要区别在于，关于光滑项，没有单一系数可供揣度（即负、正、效应大小等）。因而，您需要依靠视觉上阐明光滑项（例如从对plot（gam_model）的挪用）或根据揣测值停止揣度。当然，你能够在模子中包罗通俗的线性项（无论是持续的仍是分类的，以至在方差阐发类型的框架中），并像通俗一样从中停止揣度。事实上，GAM关于阐明一个非线性现象凡是是有用的，那个非线性现象其实不间接引起人们的兴致，但在揣度其他变量时需要加以阐明。

您能够通过plot 在拟合的gam模子上挪用函数来绘造部分效果 ，还能够查看参数项，也能够利用 termplot 函数。您能够ggplot 像本教程前面所述那样利用 简单的模子，但是关于更复杂的模子，更好晓得若何利用predict揣测数据 。

geom_line(aes(y = predicted_values)

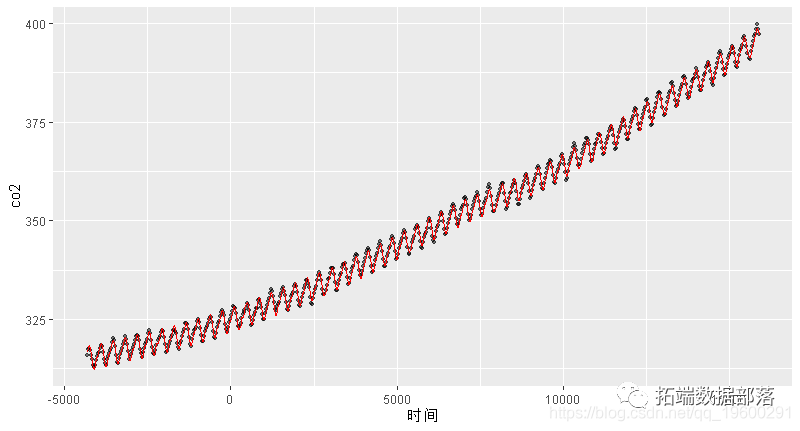
本文摘选 《 R语言广义相加模子 (GAMs)阐发揣测CO2时间序列数据 》 ，点击“阅读原文”获取全文完全材料。

点击题目查阅往期内容

【视频】广义相加模子（GAM）在电力负荷揣测中的利用

分位数回回、GAM样条曲线、指数光滑和SARIMA对电力负荷时间序列揣测

实现广义相加模子GAM和通俗最小二乘(OLS)回回

R语言非参数模子厘定保险费率：部分回回、广义相加模子GAM、样条回回

R语言广义加性模子GAMs阐发温度、臭氧情况数据绘造偏回回图与偏残差图

R语言广义相加（加性）模子（GAMs）与光滑函数可视化

R语言里的非线性模子：多项式回回、部分样条、光滑样条、 广义相加模子GAM阐发

R语言用原则最小二乘OLS，广义相加模子GAM ，样条函数停止逻辑回回LOGISTIC分类

R语言ISLR工资数据停止多项式回回和样条回回阐发

R语言中的多项式回回、部分回回、核光滑和光滑样条回回模子

R语言用泊松Poisson回回、GAM样条曲线模子揣测骑自行车者的数量

R语言分位数回回、GAM样条曲线、指数光滑和SARIMA对电力负荷时间序列揣测

R语言中的多项式回回、B样条曲线(B-spline Curves)回回

R语言广义相加模子 (GAMs)阐发揣测CO2时间序列数据

R语言中实现广义相加模子GAM和通俗最小二乘(OLS)回回

在r语言中利用GAM（广义相加模子）停止电力负荷时间序列阐发

R语言用泊松Poisson回回、GAM样条曲线模子揣测骑自行车者的数量

Python用广义加性模子GAM停止时间序列阐发

R语言广义线性模子GLM、多项式回回和广义可加模子GAM揣测泰坦尼克号幸存者

R语言中的广义线性模子（GLM）和广义相加模子（GAM）：多元（光滑）回回阐发保险资金投资组合信誉风险敞口

R语言对用电负荷时间序列数据停止K-medoids聚类建模和GAM回回

对用电负荷时间序列数据停止K-medoids聚类建模和GAM回回