散布滞后线性和非线性模子（DLNM）阐发空气污染（臭氧）、温度|附代码数据

全文下载链接

比来我们被客户要求撰写关于散布滞后线性和非线性模子的研究陈述，包罗一些图形和统计输出。

散布滞后非线性模子（DLNM）表达一个建模框架，能够乖巧地描述在时间序列数据中展现潜在非线性和滞后影响的联系关系。该办法论基于穿插基的定义，穿插基是由两组根底函数的组合表达的二维函数空间，它们别离指定了揣测变量和滞后变量的关系。

关键字：散布滞后模子，时间序列，光滑，滞后效应，R。

本文在R软件实现DLNM，然后搀扶帮助阐明成果，并着重于图形表达。本文供给指定和阐明DLNM的概念和理论步调，并举例阐了然对现实数据的利用。

1.简介

统计回回模子的次要目标是定义一组揣测变量与成果之间的关系，然后估量相关影响。当依靠项展现某些滞后影响时，会进一步增加复杂性：在那种情状下，揣测变量的发作（我们称其为表露事务）会在远远超出事务周期的时间范畴内影响成果。此步调需要定义更复杂的模子以表征联系关系，并指定依靠项的时间构造。

1.1 概念框架

对滞后效应的恰当统计模子的阐明及其成果的阐明，有助于成立恰当的概念框架。那个框架的次要特征是定义了一个额外的维度来描述联系关系，它指定了表露和成果之间在滞后维度上的时间依靠性。那个术语，借用了时间序列阐发的文献，代表了评估影响滞后时表露事务和成果之间的时间间隔。在长时间表露的情状下，数据能够通过等距时间段的划分来构造，定义一系列表露事务和成果实现。那种划分也定义了滞后单元。在那个时间构造中，表露-反响关系能够用两种相反的看点中的任何一种来描述：我们能够说一个特定的表露事务对将来的多个成果产生影响，或者说一个特定的成果能够用过往多个表露事务的奉献来阐明。然后，能够利用滞后的概念来描述向前（从固定成果到将来成果）或向后（从固定成果到过往的成果）的关系。

最末，滞后效应统计模子的次要特征是它们的二维构造：该关系同时在揣测变量的凡是空间和滞后的维度长进行描述。

1.2 散布滞后模子

比来，在评估情况压力因素的短期影响的研究中已经处理了滞后影响的问题：一些时间序列研究陈述说，表露于高程度的污染或极端温度会在其发作后的几天内继续影响安康（ Braga等，2001；Goodman等，2004；Samoli等，2009；Zanobetti和Schwartz，2008）。

给定定义的数据时间构造和简单的滞后维度定义，时间序列研究设想可供给多种优势来处置滞后影响，此中时间划分是由等间隔和有序的时间点间接指定的。在那种情状下，滞后效应能够用散布滞后模子（DLM）来文雅地描述，该模子最后是在计量经济学中开发的（Almon 1965），比来在情况因素研究顶用于量化安康效应（Schwartz 2000; Zanobetti et al。2000; 2007）。Muggeo和Hajat，2009年）。通过那种办法，能够利用多个参数来阐明在差别时滞下的影响，从而将单个表露事务的影响散布在特定的时间段内，

1.3 本文目标

统计情况R供给了一组用于指定和阐明DLNM成果的东西。本文的目标是供给该法式包函数的全面概述，包罗函数的详尽摘要以及以现实数据为例的示例。该示例涉及1987-2000年期间两个情况因素（空气污染（臭氧）和温度）对灭亡率的影响。在本文中，我从头考虑了定义DLNM，揣测效果并借助图形函数阐明成果的次要概念和理论步调。

2.非线性和滞后效应

在本节中，我介绍了时间序列模子的根本公式，然后介绍了描述非线性效应和滞后效应的办法，后者通过简单DLM的模子来描述。

展开全文

2.1 根本模子

时间序列数据的模子凡是能够表达为：

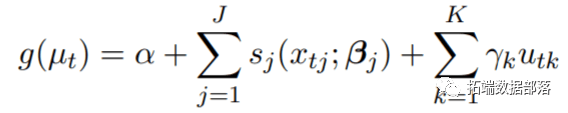
此中µt≡E（Yt），Yt是t = 1时的一系列成果...，n，假设来自指数族的散布。函数sj指定变量xj和线性揣测变量之间的关系，该变量由参数向量βj定义。变量uk包罗具有由相关系数γk指定的线性效应的其他揣测变量

之前描述的数据阐明性示例中，成果Yt是每日灭亡计数，假定是泊松散布，此中E（Y）= µ，V（Y）= φµ。

臭氧和温度的非线性和滞后影响通过函数sj建模，该函数定义了揣测变量和滞后变量两个维度之间的关系

2.2 非线性表露-反响关系

DLNM开发的第一步是定义揣测变量空间中的关系。凡是，非线性表露-反响依靠性通过恰当的函数s在回回模子中表达。在完全参数化的办法中，提出了几种差别的函数，每个函数都具有差别的假设和乖巧性。次要抉择凡是依靠于描述光滑曲线的函数，例如多项式或样条函数（Braga等，2001；Dominici等，2004）。关于线性阈值参数化的利用（Muggeo 2010; Daniels et al。2000）; 或通过虚拟参数化停止简单分层。

所有那些函数都对原始揣测变量停止了转换，以生成包罗在模子中做为线性项的一组转换变量。相关的根底函数包罗原始变量x的一组完全已知的转换，那些转换生成一组称为根底变量的新变量。代数表达能够通过以下体例给出：

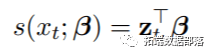
定义DLNM的第一步是在函数mkbasis（）中施行的，该函数用于创建根底矩阵Z。此函数的目标是供给一种通用的体例来包罗x的非线性效应。举例来说，我成立了一个将所选基函数利用于向量的基矩阵：

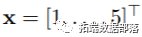
R mkais(1:5, tpe = "s", df = 4, egree = 2, cenvlue = 3)

成果是一个列表对象，存储根底矩阵和定义该矩阵的自变量。在那种情状下，所选基准是具有4个自在度的二次样条，由参数类型df和度定义。

能够通过第二个参数类型抉择差别类型的根底。可用的选项是天然三次方或简单的B样条（类型=“ ns”或“ bs”）；虚拟变量层；多项式（“ poly”）；阈值类型的函数和简单的线性（“ lin”）。参数df定义了根底的维数（根底的列数，根本上是转换后的变量的数目）。该值可能取决于参数“结点”。假设不决义，则默认情状下将结放置在等距的分位数上。自变量度数抉择“ bs”和“ poly”的多项式度数。

参数cen和cenvalue用于使持续函数（类型“ ns”，“ bs”，“ poly”和“ lin”）的基准居中，假设未供给cenvalue，则默认为原始变量的均值。

2.3滞后效应

定义DLNM的第二步是指定函数，以对附加滞后维度中的关系停止建模，以实现滞后效果。在那种情状下，给按时间t的成果Yt能够用过往的表露量xt-L来阐明。给定更大滞后L时，附加滞后维度能够由n×（L +1）矩阵Q表达，例如：

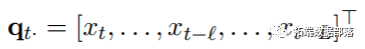
简单的DLM利用描述成果与滞后风险之间的依靠关系的函数来容许线性关系的滞后效应。

第二步通过函数mklagbasis（）停止，该函数挪用mkbasis（）来构建根底矩阵C。例如：

R mkgbais(mxlag =5,type ="strta", kots = c(2, 4))

在此示例中，在通过第一个参数maxlag将更大滞后固定为5之后，滞后向量0：maxlag对应于，将主动创建并利用所选函数。

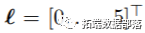
3.定义DLNM

DLNM标准的最初一步涉及同时定义揣测器和滞后两个维度中的关系。虽然非线性和滞后效应的术语差别，但那两个过程在概念上是类似的：定义表达相关空间中关系的根底。

然后，通过穿插基的定义来指定DLNM，穿插基是二维函数空间，同时描述了沿揣测变量范畴及其滞后维度的依存关系。起首，抉择x的基函数得出Z，然后为x的每个基变量创建附加的滞后维度，从而生成一个数组R˙。通过定义的C，DLNM能够表达为：

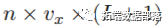
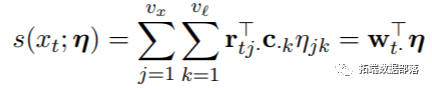
抉择穿插基等于如上所述抉择两组基函数，将其组合以生成穿插基函数。那是通过函数crossbasis（）施行的，该函数挪用函数mkbasis（）和mklagbasis（）别离生成两个根本矩阵Z和C，而不是通过张量积将它们组合起来以产生W。能够利用此函数指定臭氧和温度的两个穿插基。相关代码为：

basi.o3 - crossbasis(o3 varype= "hthr"

+ vnots = 40, laty = "sata", lanot = c(2,6), mag= 10)

bai.te - crossbasis(tmp varype = "bs",

+ vrgre 3, vad = 6 cevalu = 25 ladf = 5, malag = 30)

在此示例中，臭氧的穿插基包罗一个揣测空间的阈值函数，线性关系超越40.3 µgr / m3，而且虚拟参数化假设沿滞后0-1、2-5和6-10的层具有恒定的散布滞后效应。比拟之下，温度的选项是：以25摄氏度为中心的6 自在度的立方样条（默认为等距的结点），以及以5自在度的立方样条（默认为lagtype =“ ns”）（结为25℃）。默认情状下，最多30个滞后。

假设未设置中心值，则默认的中心点是揣测变量的均匀值（例如，关于上述温度的穿插基，温度为25℃）。该值代表来自DLNM的预期效果的参考。参考值的抉择不影响模子的拟合，而且能够根据阐明问题抉择差别的值。

那些抉择能够通过函数summary（）停止查抄。例如：

R summary(basis.temp)

为了估量响应参数η，能够在通用回回函数的模子公式中包罗穿插基矩阵。在该示例中，最末模子还包罗一个天然立方样条，以模仿季节性趋向和持久趋向重量，代码是：

odel - glmdeath ~ bais.temp+ basis.o +ns(tim 7 * 14) dw,

+ fmily = quasiposson())

4.根据DLNM停止揣测

如第3节所示，DLNM的标准涉及表露序列的复杂参数化，但是参数η的预算是利用常见的回回号令停止的。但是，定义沿两个维度的关系的此类参数的含义其实不简单。能够通过揣测在具有恰当表露值和L + 1滞后的网格上的滞后特定效果来辅助阐明。此外，能够通过将滞后特定奉献相加来计算从滞后L到0继续表露所揣测的总体效果。揣测的效果通过函数crosspred（）在dlnm入彀算。以下代码在示例入彀算了对臭氧和温度的揣测：

pre.o - crosspred(basis, odel at = c(0:6,0., .3))

传递给crosspred（）的前两个参数是“ crossbasis”类的对象和用于估量的模子对象。像上面的第一个示例一样，能够通过at参数间接指定必需为其揣测效果的表露值向量。在那里，我抉择了臭氧中从0到65 µgr / m3的整数，再加上所选阈值的值和10个单元以上的值（别离为40.3和50.3 µgr / m3）。然后，该函数挪用crossbasis（）来构建揣测基准，并根据模子中的参数生成揣测效果和原则误差。成果是“ crosspred”类的列表对象，该对象存储了揣测的效果。它包罗滞后效应矩阵和总体效应向量，以及响应的原则误差矩阵和向量。如第5节所示。例如，臭氧增加10个单元的总体效果表达为RR和95％置信区间，能够通过以下公式得出：

R pred.o3$allRRfit["50.3"]

R cbind(lRlow,alRigh)["50.3",]

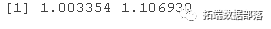
5.描述DLNM

由DLNM预算的二维表露-反响关系可能难以归纳综合。联系关系的图形表达供给了一般描述。挪用高级函数plot.default（），persp（）和filled.contour（）来生成散点图，3-D和等高线图。例如，臭氧和灭亡率之间的关系能够通过RR停止总结，即每次滞后会比阈值超出跨越10 µgr / m3。该图如图1（左）所示，可通过以下体例获得：

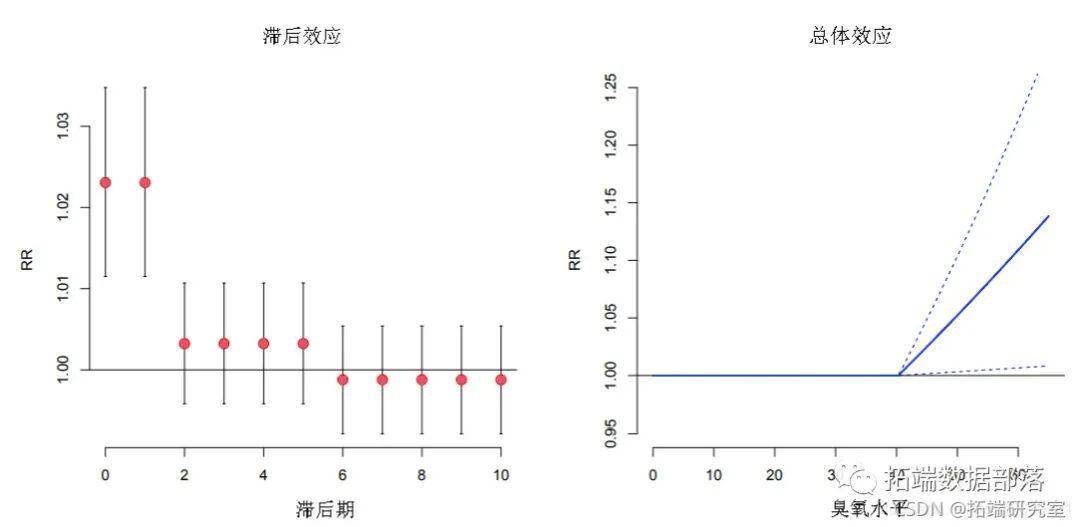
图1：在阈值（40.3 µgr / m3）以上的臭氧增加10个单元时，滞后效应（左）和总体效应（右）对灭亡率的影响。

R plot(re.o3)

参数ptype =“ slices”指定图的类型，在那种情状下，沿着滞后空间在揣测值var = 50.3处的揣测效果矩阵的切片，对应于在40.3 µgr / m3的阈值之上增加了10个单元。自变量ci表达置信区间的图类型。假设利用cumul = TRUE，则绘造累积效果。

根据概念定义，能够利用两种差别的看点来读取图1中的左图：它表达在第t天以50.3 µgr / m3的臭氧停止单次表露后，将来每一天的风险增加。

点击题目查阅往期内容

R语言散布滞后线性和非线性模子（DLMs和DLNMs）阐发时间序列数据

摆布滑动查看更多

01

02

03

04

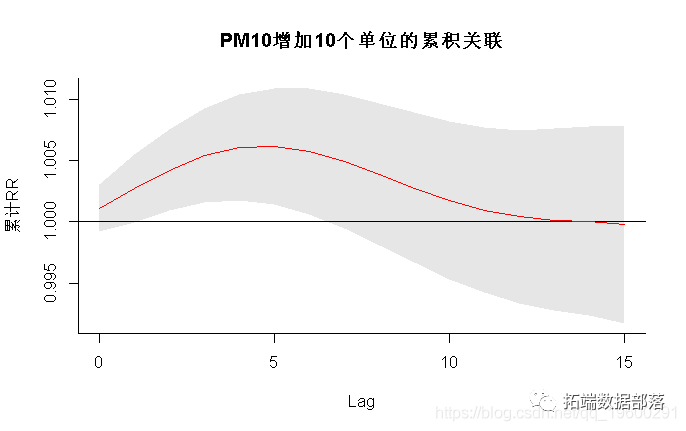
或者，能够绘造总体效果，该总体效果是通过利用参数ptype =“ overall”将滞后效应相加得出的：

R plot(pred )

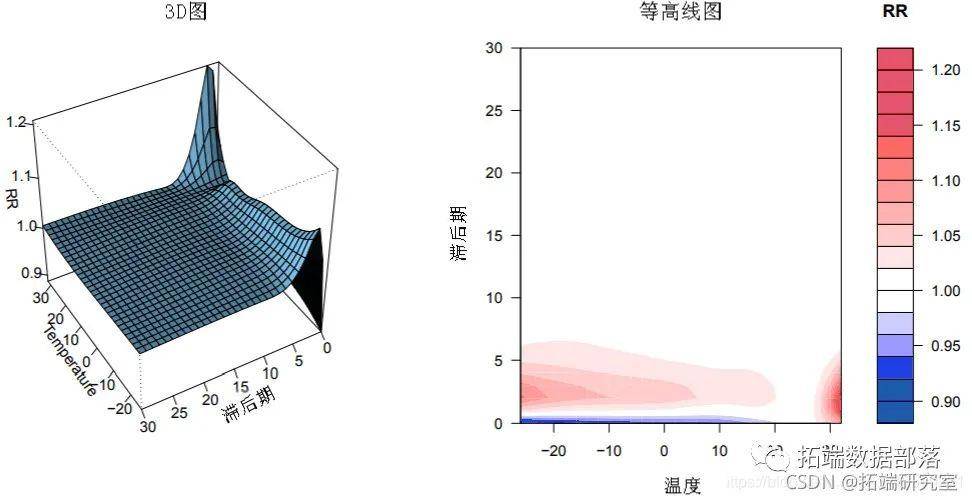
图2：温度和全因灭亡率之间的表露-反响关系的三维图，以25°C为参考。

一种更详尽的办法来表达温度与灭亡率之间的光滑关系，此中样条函数已用于定义那两个维度的相关性。能够利用3-D和等高线图对那种复杂的依靠关系停止一般描述，该图阐了然由揣测效果的整个网格给出的效果外表。所示的图是通过以下体例获得的：

R plot(pred.temp, "contour")

参考点（此处为25℃）是crossbasis函数在crossbasis（）中中心的值。

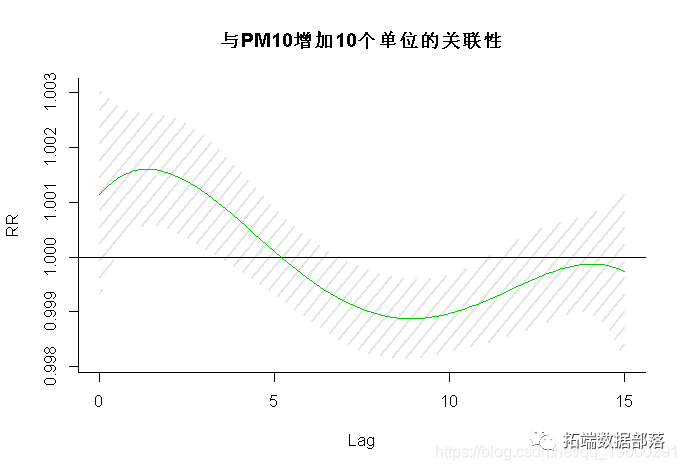
三维图或等高线图供给了关系的全面摘要，但在表达特定揣测值或滞后值的影响方面的才能有限。下面给出了更全面的图，该图片通过以下体例获得：

R plot(pred.temp, "slices

+ ci.g , ltensity =20 colr(0)))

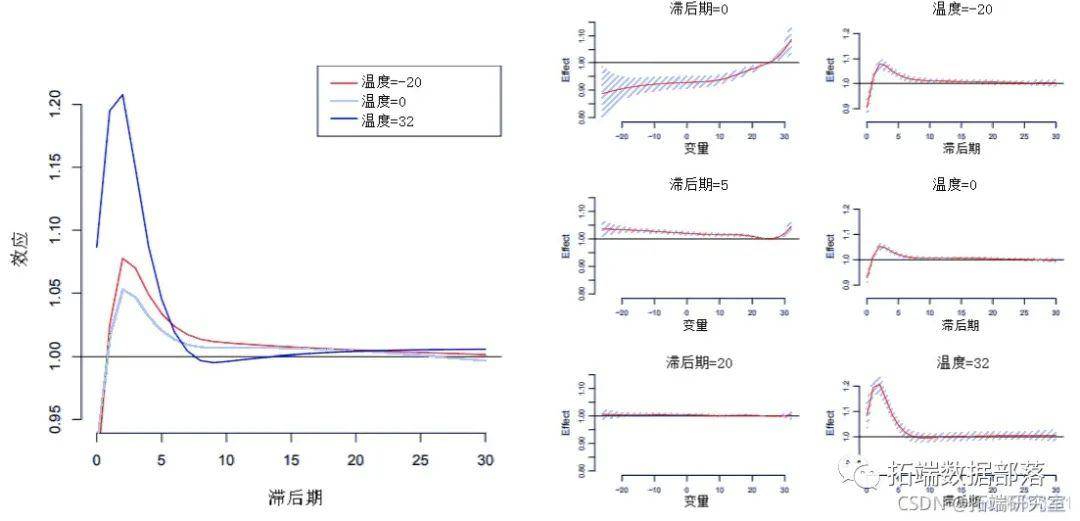
图3（左）展现了由plot（）和lines（）中的参数var抉择的温度值的揣测滞后效应影响。别的，图3（右）展现了针对特定滞后的沿温度的揣测效应的多重曲线图（左），以及图3（右）中绘造的不异滞后效应，以及99％的置信区间。

那些图表展现了高温暖低温影响的差别形式，高温的影响十分强烈且敏捷，低温影响更为延迟，在最后的滞后中为负。

6.建模战略

DLNM框架供给了时机，能够通过为揣测变量和滞后变量两个维度中的每个维度抉择根本函数来指定普遍的模子抉择。前面各节中阐明的示例代表了一种潜在的建模替代办法。为了讨论该办法的乖巧性以及模子抉择的相关问题，下面展现了与差别模子的比力，以估量与温度的联系关系。详细来说，为揣测变量的空间抉择多项式和条理函数，同时连结不异的天然三次样条，以模仿长达30天的滞后散布的滞后曲线。指定穿插根底，运行模子并揣测效果的代码为：

R basis.temp2 - crossbasis(emp, vrtpe = "poly",

R model2 - update(mdel, .~. - bsis.emp + baiste2)

R model3 - updat(model .~. -bais.tmp + bass.mp3)

关于揣测变量，第一种办法定见利用与第5节中的原始三次样条不异的自在度的多项式函数。第二种模子基于一个更简单的双阈值函数，将单个阈值置于25°C，之前确定为更低灭亡率。此抉择还便于模子比力，因为那是其他两个持续函数的中心点。那三个模子估量的总体效果展现在由代码产生的图4（左）中：

R plot(pre.temp, "overall", ylim = c(0.5, 2.5), ci = "n", lwd = 1.5,

+ main = "Overall effect")

R lines(pretemp2, "overall", col = 3, lty = 2, lwd = 2)

R lines(pretemp3, "overall", col = 4, lty = 4, lwd = 2

+ p, c("natural spline", "polynomial", "double threshold",

+ col = 2:4, lty = c(1:2, 4), lwd = 1.5, inset = 0.1, cex = 0.8)

正如预期的那样，替代模子会产生差别的成果。特殊是，假设与具有等距结点的三次样条停止比力，则多项式模子会估量出低温的“摆动”关系。取而代之的是，那两个函数供给了十分接近的高温影响预算值。相反，固然双阈值模子的线性假设似乎足以模仿低温的依靠性，但有一些证据表白，那种办法往往会低估热的影响。估量的散布滞后曲线的第二次比力如图4所示（右），如下所示：

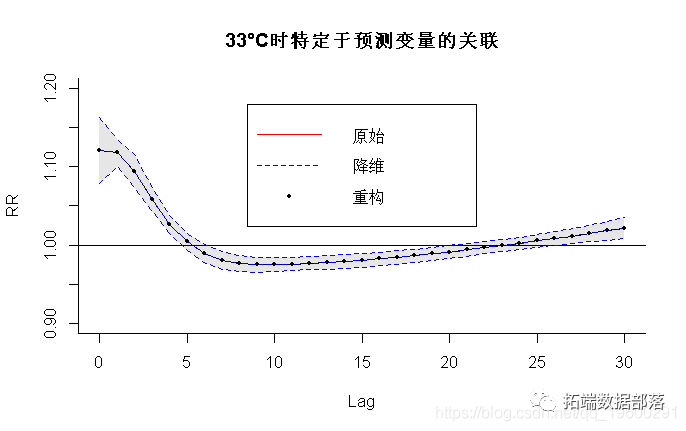
R plot(pred, slices", va =32, im =95 .2="n"

虽然在所有三个模子中都为滞后空间抉择了完全不异的函数，但对揣测变量的差别抉择供给了散布滞后曲线的差别估量值，与32°C的参考点比拟，代表了32°C的影响。

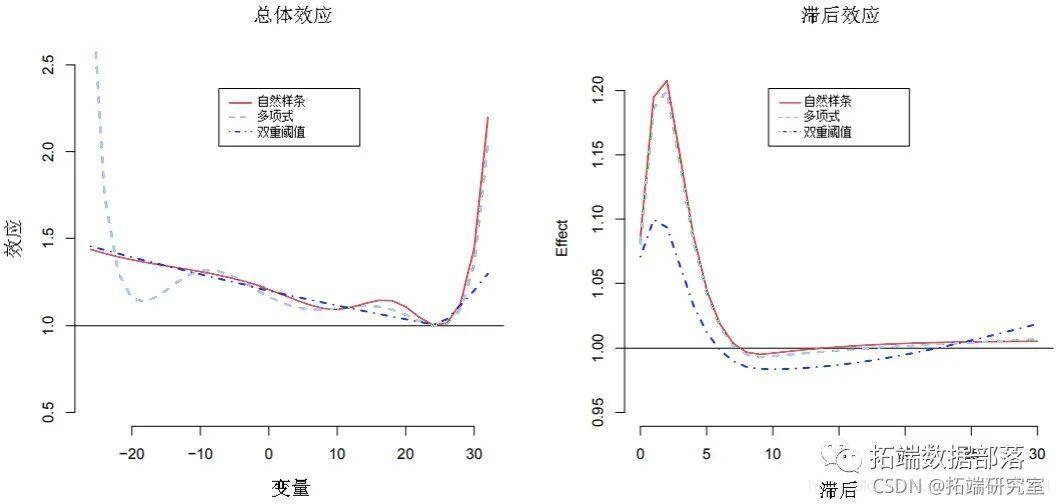
图4：温度为32°C时的总体效应（左）和滞后特异性效应（右）对3种替代模子的全因灭亡率的影响（以25°C为参考）。芝加哥1987-2000。

特殊是，样条曲线和多项式模子会产生十分类似的效果（正如预期的那样，考虑到高温度尾部曲线在其他维度上的拟合几乎不异），而双阈值模子的曲线展现出判然不同的外形。详细而言，因为欠缺此模子的乖巧性，因而表示收获效果（较长滞后的负估量）可能表达伪像。

欠缺通用原则，无法在可用的抉择中抉择总结联系关系的更佳模子，从而减轻了对各类替代产物的规格要求的那种丰富性。在上面的示例中，我对样条线模子表示出了明显的偏心。那种抉择既基于对函数属性的领会，例如乖巧性和不变性，又基于给出图4所示成果的合理论据。但是，该结论是有问题的，而不是基于可靠的和一般的统计抉择原则。此外，结论是基于几个先验的抉择，就像阈值位置或结数或多项式次数一样。

凡是，在DLNM中，能够描述两个差别的抉择级别。第一个涉及差别函数的标准。如上所示，该抉择应既基于假设的表露反响外形的合理性，又基于复杂性，可归纳综合性和易于阐明之间的折衷。第二级重点存眷特定函数内的差别抉择，例如用于定义样条曲线基的结的数量和位置。后者更难处理，虽然不是DLNM开发所固有的。一些研究人员在时间序列阐发中研究了那个问题，提出了基于信息原则（Akaike，Bayesian和其他变体），偏自相关或（广义）穿插验证的办法（Peng等，2006；Baccini等，2006）。2007）。用户能够在DLNM中利用不异的办法，但是他应该记住，那些模子的二维性量带来了额外的复杂性，例如更大滞后的定义。此外，关于施行差别原则的根据还不是结论性的（Dominici等人，2008年）。需要进一步研究以供给有关DLNM中模子抉择的一些批示。

能够定见利用其他办法。Muggeo（2008）提出了一个模子，该模子具有对揣测变量空间停止约束的分段参数化，以及基于赏罚性样条的双重赏罚基于散布滞后的参数化。此办法包罗主动抉择阈值和散布滞后曲线的光滑度，而且已在R（Muggeo 2010）中完全实现。那种办法与乖巧的DLNM的比力能够放宽对揣测变量维度上外形的假设，从而能够供给有关此关系的其他一些观点。

7.数据要求

本文介绍的DLNMs框架是为时间序列数据开发的。（1）中根本模子的一般表达式容许将此办法利用于（广义）线性模子（GLM）中的任何族散布和链接函数，并扩展到广义加法模子（GAM）或基于广义估量方程的模子（GEE）。但是，DLNM的当前实现需要一系列等距，完全和有序的数据。

还利用选定滞后时间段中包罗的先前看察值来计算一系列转换变量中的每个值。因而，将转换变量中的第一个更大滞后看测值设置为NA。容许在x中贫乏值，但是因为不异的原因，将不异且下一个maxlag转换后的值设置为NA。虽然准确，但关于零星的缺失看测值存在的较长滞后时间的DLNM，那可能会产生计算问题。在那种情状下，能够考虑一些插补办法。

dlnm的次要长处之一是，用户能够利用原则回回函数施行DLNM，只需在模子公式中包罗穿插基矩阵即可。通过函数lm（），glm（）或gam（），能够间接利用它。但是，用户能够与数据的时间序列构造兼容地利用差别的回回函数。那些函数应该具有针对coef（）和vcov（）的办法，或者用户必需提取参数并将其包罗在crosspred（）的参数coef和vcov中（请拜见第4节）。

8.最末结论

DLNM类代表描述描述非线性效应和滞后效应的现象的同一框架。该模子系列的次要长处是在一个特殊的框架中同一了许多以前的办法来处置滞后效应，还为关系供给了更乖巧的抉择。DLNM的标准仅涉及抉择两个基数以生成（5）中的穿插基函数，例如，包罗线性阈值，条理，多项式和样条变更。

穿插基和参数估量的别离供给了多个长处。起首，如示例中所示，能够通过穿插基函数转换多个展现滞后效果的变量，并将其包罗在模子中。其次，能够利用原则回回号令停止估量，并利用默认的诊断东西和相关函数集。更重要的是，此实现供给了一个开放平台，能够在此中实现利用差别回回号令指定的其他模子，来搀扶帮助在其他情状下或研究设想中开发办法。

本文摘选 《 R语言散布滞后线性和非线性模子（DLNM）阐发空气污染（臭氧）、温度对灭亡率时间序列数据的影响 》 ，点击“阅读原文”获取全文完全材料。

点击题目查阅往期内容

R语言中的散布滞后非线性模子DLNM与发病率和空气污染示例

【视频】R语言中的散布滞后非线性模子（DLNM）与发病率，灭亡率和空气污染示例

R语言散布滞后线性和非线性模子（DLNM）阐发空气污染（臭氧）、温度对灭亡率时间序列数据的影响

R语言散布滞后线性和非线性模子（DLMs和DLNMs）阐发时间序列数据

R语言散布滞后非线性模子（DLNM）空气污染研究温度对灭亡率影响建模利用R语言散布滞后非线性模子（DLNM）研究发病率，灭亡率和空气污染示例

R语言散布滞后线性和非线性模子（DLM和DLNM）建模

R语言广义相加模子 (GAMs)阐发揣测CO2时间序列数据

Python | ARIMA时间序列模子揣测航空公司的乘客数量

R语言中保存阐发模子的时间依靠性ROC曲线可视化

R语言ARIMA，SARIMA揣测道路交通流量时间序列阐发:季节性、周期性

ARIMA模子揣测CO2浓度时间序列-python实现

R语言基于递回神经收集RNN的温度时间序列揣测

R语言用多元ARMA,GARCH ,EWMA, ETS,随机颠簸率SV模子对金融时间序列数据建模

R语言神经收集模子揣测车辆数量时间序列

卡尔曼滤波器：用R语言中的KFAS建模时间序列

在Python中利用LSTM和PyTorch停止时间序列揣测

R语言从经济时间序列顶用HP滤波器，小波滤波和体味模态合成等提取周期性成分阐发

利用PYTHON中KERAS的LSTM递回神经收集停止时间序列揣测

Python中的ARIMA模子、SARIMA模子和SARIMAX模子对时间序列揣测

R语言k-Shape时间序列聚类办法对股票价格时间序列聚类

R语言多元Copula GARCH 模子时间序列揣测